Resolución de ejercicios: Complemento ortogonal de un subespacio
Descubre cómo encontrar el complemento ortogonal de un subespacio en el fascinante mundo de la resolución de ejercicios matemáticos. En este artículo, exploraremos paso a paso este concepto fundamental en álgebra lineal que te permitirá comprender mejor las relaciones entre vectores y subespacios. ¡Acompáñanos en este viaje de descubrimiento matemático en Polaridades!
Aprendiendo a calcular el complemento ortogonal: guía paso a paso
El complemento ortogonal de un subespacio vectorial es un concepto fundamental en el ámbito de álgebra lineal y geometría. Para calcular el complemento ortogonal de un subespacio, se siguen varios pasos que resultan clave para comprender y aplicar este concepto de manera efectiva. A continuación, se presenta una guía paso a paso para aprender a calcular el complemento ortogonal:
- Paso 1: Comprender el concepto de espacio ortogonal.
- Paso 2: Identificar el subespacio del que se desea encontrar el complemento ortogonal.
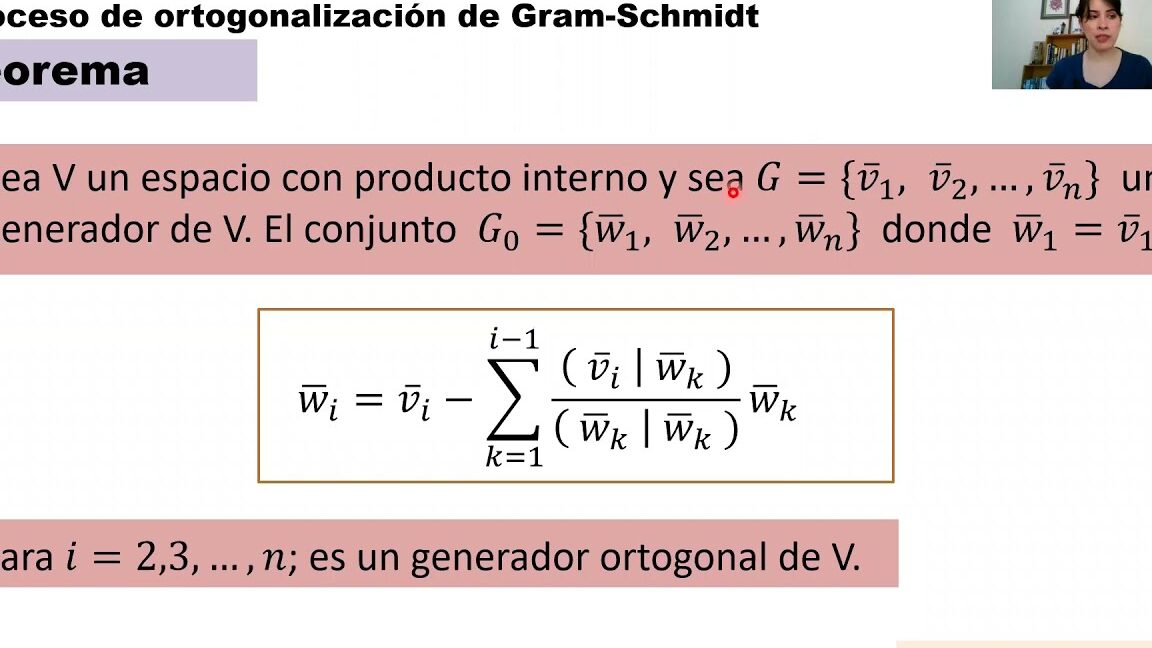
- Paso 3: Calcular una base ortogonal para el subespacio dado.
- Paso 4: Utilizar la base ortogonal para formar una matriz ortogonal.
- Paso 5: Calcular la matriz transpuesta de la matriz ortogonal.
- Paso 6: Determinar el complemento ortogonal como el espacio nulo de la matriz transpuesta.
Este proceso paso a paso proporciona una metodología clara y sistemática para encontrar el complemento ortogonal de un subespacio vectorial. Al dominar estos pasos, se adquiere una comprensión más profunda de la geometría vectorial y sus aplicaciones en diversos campos de las matemáticas y la física.
Determinando la ortogonalidad entre dos subespacios: métodos y ejemplos.
Determinando la ortogonalidad entre dos subespacios: métodos y ejemplos
En álgebra lineal, la ortogonalidad entre dos subespacios juega un papel crucial en diversos campos, desde la geometría hasta el procesamiento de señales. Determinar si dos subespacios son ortogonales puede proporcionar información valiosa sobre la estructura de un sistema.
Métodos para determinar la ortogonalidad entre dos subespacios:
- Producto escalar: Uno de los métodos más comunes es verificar si el producto escalar de cualquier par de vectores, uno de cada subespacio, es igual a cero. Si esto se cumple para todos los pares de vectores, los subespacios son ortogonales.
- Proyecciones ortogonales: Otra forma de determinar la ortogonalidad es a través de las proyecciones ortogonales. Si las proyecciones de un subespacio sobre el otro son todas cero, entonces los subespacios son ortogonales.
- Descomposición en valores singulares: La descomposición en valores singulares puede ser útil para determinar la ortogonalidad entre subespacios al analizar las matrices asociadas a dichos subespacios.
Ejemplos de determinación de ortogonalidad entre subespacios:
| Ejemplo | Método utilizado |
|---|---|
| Espacio vectorial tridimensional | Producto escalar |
| Subespacios generados por funciones ortogonales | Proyecciones ortogonales |
| Descomposición en valores singulares de una matriz | Descomposición en valores singulares |
Entendiendo la proyección ortogonal: pasos para determinarla
La proyección ortogonal es un concepto fundamental en geometría que se utiliza para encontrar la distancia entre un punto y un plano. Para determinar la proyección ortogonal de un punto sobre un plano, se deben seguir los siguientes pasos:
1. **Calcular el vector director del plano**: Para encontrar la proyección ortogonal de un punto sobre un plano, primero es necesario conocer un vector normal al plano, el cual nos indicará la dirección perpendicular al mismo.
2. **Obtener el vector director del punto al plano**: Una vez se tiene el vector normal al plano, se debe calcular el vector que une el punto dado con cualquier punto del plano. Este vector es crucial para encontrar la proyección ortogonal.
3. **Calcular el producto escalar**: El siguiente paso consiste en hallar el producto escalar entre el vector director del plano y el vector que une el punto con el plano. Este producto escalar nos dará la longitud de la proyección ortogonal.
4. **Determinar la proyección ortogonal**: Finalmente, para obtener la proyección ortogonal en sí, se debe dividir el producto escalar calculado en el paso anterior por la magnitud del vector director del plano.
Siguiendo estos pasos, es posible determinar con precisión la proyección ortogonal de un punto sobre un plano, lo que resulta de gran utilidad en diversos contextos matemáticos y geométricos.













Post Comment