Las distintas dimensiones de los vectores: espacio vectorial vs subespacio vectorial
Descubre en este artículo las diferencias entre un espacio vectorial y un subespacio vectorial, dos conceptos fundamentales en el ámbito matemático. Acompáñanos en un viaje por las distintas dimensiones de los vectores y desentraña sus fascinantes propiedades. ¡Sumérgete en el mundo de las polaridades matemáticas en Polaridades!
Explorando los conceptos de espacios y subespacios vectoriales
Un espacio vectorial es un conjunto de elementos, llamados vectores, que cumplen ciertas propiedades algebraicas. Estos espacios son fundamentales en álgebra lineal y tienen aplicaciones en diversas áreas de las matemáticas y la física.
Características de un espacio vectorial:
- Cerrado bajo la suma de vectores.
- Cerrado bajo la multiplicación por escalares.
- Posee un vector nulo.
- Para cada vector, existe su opuesto.
Un subespacio vectorial es un subconjunto de un espacio vectorial que, por sí mismo, es un espacio vectorial con las mismas operaciones definidas en el espacio vectorial original. Para que un subconjunto sea considerado un subespacio vectorial, debe cumplir con las siguientes condiciones:
- Contener al vector nulo.
- Ser cerrado bajo la suma de vectores.
- Ser cerrado bajo la multiplicación por escalares.
La noción de subespacios vectoriales es importante en el estudio de la estructura de los espacios vectoriales, ya que permiten analizar propiedades específicas de conjuntos más pequeños dentro de un espacio vectorial más grande.
Determinando la dimensión de un subespacio: ¿Cómo calcularla correctamente?
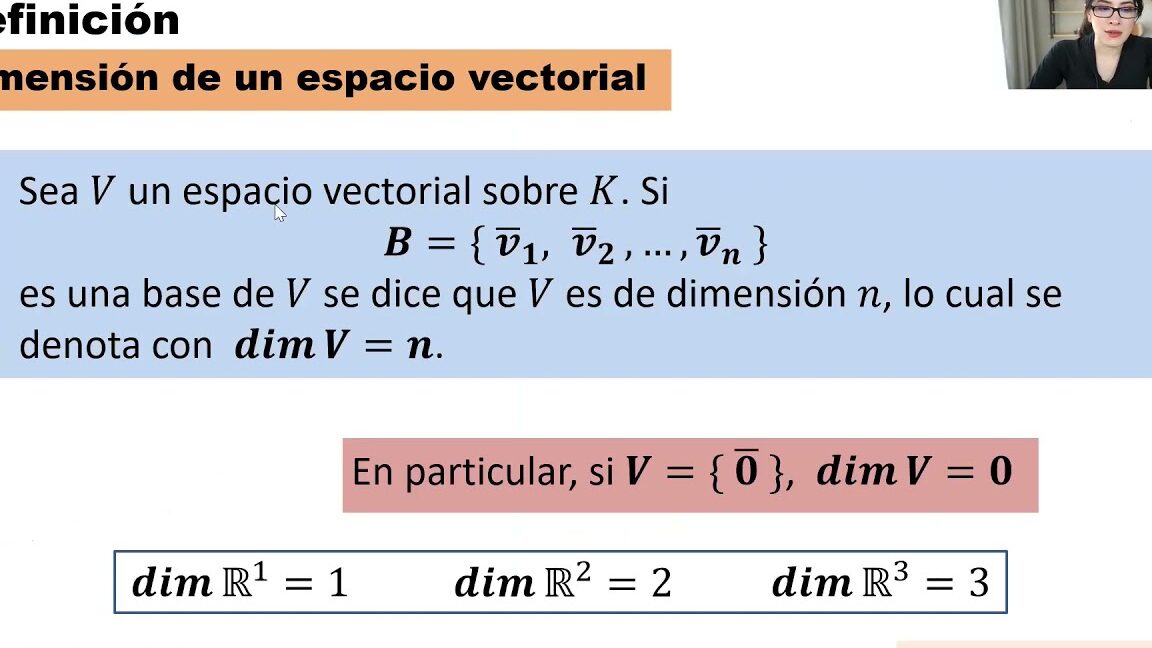
Al determinar la dimensión de un subespacio, es fundamental seguir ciertos pasos para calcularla correctamente. La dimensión de un subespacio vectorial se define como el número de vectores linealmente independientes que lo generan.
Para calcular la dimensión de un subespacio, se pueden seguir los siguientes pasos:
- Identificar una base para el subespacio: Una base es un conjunto de vectores linealmente independientes que generan el subespacio. Encontrar una base es esencial para determinar la dimensión.
- Contar el número de vectores en la base: La cantidad de vectores en la base será igual a la dimensión del subespacio. Esta cantidad es un número entero no negativo.
- Verificar si es posible expresar cualquier otro vector del subespacio como combinación lineal de los vectores de la base. Si es posible, los vectores de la base son linealmente independientes y forman una base.
Es importante recordar que la dimensión de un subespacio es un concepto fundamental en álgebra lineal y tiene aplicaciones en diversos campos de las matemáticas y la física.
Entendiendo los subespacios en un espacio vectorial de dimensión finita
En un espacio vectorial de dimensión finita, un subespacio es un subconjunto que cumple con ciertas propiedades que lo hacen comportarse como un espacio vectorial por sí mismo. Para comprender mejor este concepto, es importante tener en cuenta lo siguiente:
- Un subespacio debe contener al vector nulo.
- La suma de dos vectores en el subespacio debe dar como resultado otro vector en el mismo subespacio.
- El producto de un escalar por un vector en el subespacio también debe pertenecer al subespacio.
Tipos de subespacios
En un espacio vectorial de dimensión finita, es posible encontrar diferentes tipos de subespacios, entre los cuales destacan:
| Subespacio | Definición |
|---|---|
| Subespacio generado | Es el conjunto de todas las combinaciones lineales de un conjunto dado de vectores. |
| Subespacio nulo | Conjunto que consta únicamente del vector nulo. |
| Subespacio complementario | Subespacio que, sumado a otro subespacio, da como resultado el espacio vectorial completo. |
Importancia de los subespacios
Comprender los subespacios en un espacio vectorial de dimensión finita es fundamental en ámbitos como el álgebra lineal y la geometría, ya que permiten estudiar de manera más estructurada las propiedades y relaciones entre los vectores. Además, el análisis de subespacios resulta útil en la resolución de sistemas de ecuaciones lineales y en la representación de transformaciones lineales.
¡Y así es como los vectores se dan una vuelta por el espacio vectorial y deciden instalarse en su acogedor subespacio vectorial para descansar de tanto cálculo! Ya sabes, en el mundo de las matemáticas, hasta los vectores necesitan su ratito de relax. ¡Hasta la próxima, dimensiones matemáticas!












Post Comment