Explorando los espacios vectoriales generados por una matriz
Descubre la fascinante geometría detrás de los espacios vectoriales generados por una matriz. En este artículo exploraremos cómo una matriz puede crear un universo de posibilidades en el mundo de las matemáticas. ¡Acompáñanos en este viaje de descubrimiento!
Determinando si un conjunto de matrices forma un espacio vectorial
En el ámbito matemático, para determinar si un conjunto de matrices forma un espacio vectorial, es necesario comprobar que cumpla con ciertas propiedades fundamentales.
Para que un conjunto de matrices forme un espacio vectorial, debe cumplir con las siguientes condiciones:
- Cerrado bajo la suma: La suma de dos matrices del conjunto debe dar como resultado otra matriz dentro del mismo conjunto.
- Cerrado bajo el producto por un escalar: El producto de una matriz del conjunto por un escalar debe pertenecer al conjunto.
- Existencia de elemento neutro: Debe haber una matriz en el conjunto que actúe como elemento neutro respecto a la suma de matrices.
- Existencia de inverso aditivo: Cada matriz en el conjunto debe tener una matriz opuesta que, al sumarse, dé como resultado el elemento neutro.
Es importante destacar que si un conjunto de matrices cumple con estas propiedades, entonces se puede afirmar que forma un espacio vectorial. En caso contrario, si no se cumplen una o más de estas condiciones, el conjunto no será considerado un espacio vectorial.
Espacio vectorial: concepto y aplicación en la geometría euclidiana
Un espacio vectorial es una estructura matemática que consiste en un conjunto de elementos, llamados vectores, junto con dos operaciones: la suma de vectores y la multiplicación de un vector por un escalar. En el contexto de la geometría euclidiana, los espacios vectoriales son fundamentales para el estudio de figuras geométricas y transformaciones en el plano o el espacio tridimensional.
Algunos conceptos clave sobre los espacios vectoriales en geometría euclidiana son:
- Vector: Un vector es una entidad que tiene magnitud y dirección. En geometría euclidiana, los vectores se utilizan para representar desplazamientos, fuerzas, velocidades, etc.
- Suma de vectores: La suma de dos vectores se realiza sumando componente a componente. Geométricamente, la suma de dos vectores se representa mediante el método del paralelogramo.
- Multiplicación por un escalar: La multiplicación de un vector por un escalar consiste en multiplicar cada componente del vector por dicho escalar. Esta operación permite cambiar la magnitud del vector sin alterar su dirección.
- Independencia lineal: Un conjunto de vectores es linealmente independiente si ninguno de ellos puede expresarse como combinación lineal de los demás. En geometría euclidiana, la independencia lineal es crucial para determinar la base de un espacio vectorial.
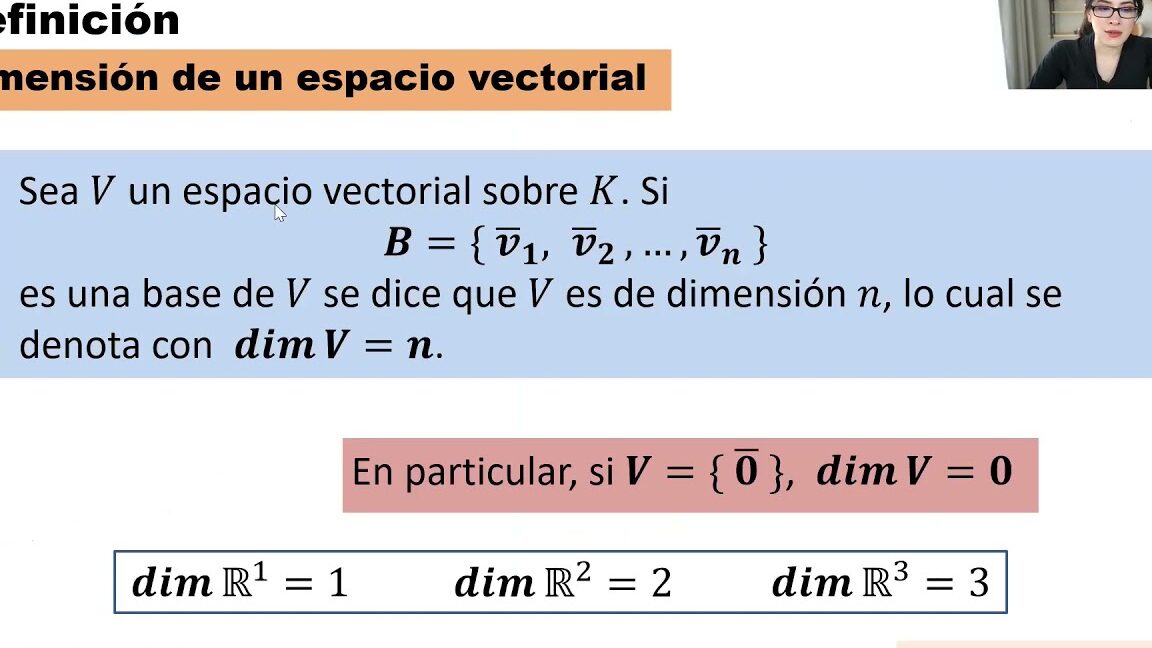
- Base y dimensión: La base de un espacio vectorial es un conjunto de vectores linealmente independientes que generan todo el espacio mediante combinaciones lineales. La dimensión de un espacio vectorial es el número de vectores en su base.
: La cantidad de vectores necesaria para generar R3
| Número de Vectores | Resultados |
|---|---|
| 1 | No es suficiente, solo genera una recta. |
| 2 | Es suficiente, genera un plano en R3. |
| 3 o más | Es suficiente, genera todo el espacio tridimensional R3. |
Descubre todos los secretos de los espacios vectoriales generados por una matriz y conviértete en el «Matrix Master». ¡Hasta Neo estaría orgulloso de tus habilidades matriciales! ¡No hay ecuación que se te resista ahora!












Post Comment