Cómo resolver desigualdades lineales en cálculo diferencial
Las desigualdades lineales son una herramienta fundamental en el cálculo diferencial. Resolverlas puede parecer complicado al principio, pero en realidad es más sencillo de lo que parece. En este artículo, te mostraremos paso a paso cómo resolver desigualdades lineales y cómo aplicar este conocimiento en problemas reales. Si estás listo para adentrarte en el mundo de las desigualdades lineales, ¡continúa leyendo!
Cómo resolver una desigualdad lineal paso a paso
Cómo resolver desigualdades lineales en cálculo diferencial
En el cálculo diferencial, las desigualdades lineales son una parte fundamental para comprender el comportamiento de las funciones y sus intervalos de crecimiento o decrecimiento. Resolver una desigualdad lineal paso a paso puede ser una tarea sencilla si se siguen ciertos pasos y se utilizan las herramientas adecuadas. En este artículo, te explicaremos detalladamente cómo resolver una desigualdad lineal paso a paso.
Paso 1: Identificar el tipo de desigualdad lineal
Lo primero que debes hacer es identificar si la desigualdad es del tipo «menor que» (). Dependiendo del símbolo de desigualdad utilizado, se seguirán diferentes pasos para resolverla.
Paso 2: Aislar la variable
Una vez identificado el tipo de desigualdad, debes aislar la variable en un lado de la ecuación. Para ello, puedes utilizar operaciones algebraicas como sumar, restar, multiplicar o dividir ambos lados de la ecuación por el mismo valor. Recuerda que si realizas una operación en un lado de la desigualdad, debes hacer lo mismo en el otro lado para mantener el equilibrio.
Ejemplo:
Si tenemos la desigualdad 2x + 3 > 9, podemos aislar la variable de la siguiente manera:
2x > 9 – 3
2x > 6
Paso 3: Dividir o multiplicar por un número negativo
Si al aislar la variable obtienes un coeficiente negativo, debes tener en cuenta que al multiplicar o dividir por ese valor, el sentido de la desigualdad se invierte. Es decir, si divides por un número negativo, debes cambiar el sentido de la desigualdad.
Ejemplo:
Si tenemos la desigualdad -3x -5
Paso 4: Representar la solución en la recta numérica
Una vez que has resuelto la desigualdad y obtenido el valor de la variable, debes representar la solución en la recta numérica. Para ello, debes marcar el valor de la variable como un punto cerrado o abierto, dependiendo de si el símbolo de desigualdad es «menor que o igual a» (≤) o «mayor que o igual a» (≥).
Qué es una desigualdad lineal y ejemplos
Qué es una desigualdad lineal y ejemplos
Una desigualdad lineal es una expresión matemática que compara dos cantidades utilizando los símbolos de mayor que (>), menor que (Identificar la variable: En primer lugar, se debe identificar la variable o incógnita en la desigualdad. Por ejemplo, en la desigualdad 3x + 2 Despejar la variable: El siguiente paso es despejar la variable de la desigualdad. Para esto, se deben realizar operaciones matemáticas para aislar la variable en un lado de la desigualdad. Por ejemplo, para despejar x en la desigualdad anterior, se resta 2 de ambos lados y se divide por 3, obteniendo x Representación gráfica: Una vez que se ha resuelto la desigualdad, se puede representar gráficamente en una recta número. Para ello, se dibuja una línea vertical en el valor de la solución encontrada y se sombrea el área correspondiente a la desigualdad. En el ejemplo anterior, se representa una línea vertical en x = 2 y se sombrea el área a la izquierda de la línea.
4. Verificación: Finalmente, se verifica si la solución encontrada satisface la desigualdad original. Para hacer esto, se sustituye la solución en la desigualdad y se comprueba si se cumple. Si se cumple, entonces la solución es válida; de lo contrario, se debe buscar otra solución.
A continuación, se muestran algunos ejemplos de desigualdades lineales:
– 2x + 5 > 7: El valor de x debe ser mayor que 1 para que la desigualdad sea verdadera.
– 3x – 4 ≤ 10: El valor de x debe ser menor o igual a 14 para que la desigualdad sea verdadera.
– -2x + 3 ≥ -6: El valor de x debe ser mayor o igual a 4.5 para que la desigualdad sea verdadera.
Qué es una desigualdad y cómo se resuelve
Qué es una desigualdad y cómo se resuelve
Las desigualdades son expresiones matemáticas que comparan dos cantidades o expresiones y establecen una relación de orden entre ellas.
¡Así que ahí tienes! Ahora eres un maestro en la resolución de desigualdades lineales en cálculo diferencial. ¿Quién sabía que las matemáticas podían ser tan emocionantes? Ahora puedes enfrentarte a cualquier desigualdad con confianza y decirle adiós a esas incógnitas rebeldes. ¡Adiós desigualdades, hola ecuaciones resueltas! Mantén tu calculadora cerca y prepárate para ser el héroe matemático en tu clase. ¡Nunca más te sentirás desigual en el mundo del cálculo diferencial!
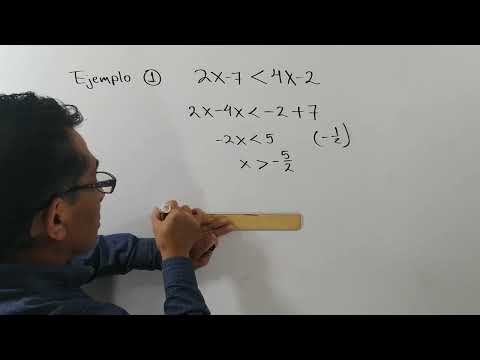














Post Comment