Cómo calcular la ecuación de una circunferencia con centro en el origen

La ecuación de una circunferencia con centro en el origen es una herramienta fundamental en el mundo de la geometría y las matemáticas. Permite describir de manera precisa y concisa la forma y posición de una circunferencia en un plano cartesiano. En este artículo, te mostraremos paso a paso cómo calcular esta ecuación, brindándote las bases necesarias para comprender y aplicar este concepto de manera efectiva. ¡Prepárate para sumergirte en el fascinante mundo de las circunferencias y descubrir cómo utilizar esta ecuación en tus propios proyectos!

Cómo hallar la ecuación de la circunferencia con centro en el origen

Cómo calcular la ecuación de una circunferencia con centro en el origen

En este artículo vamos a explicar paso a paso cómo hallar la ecuación de una circunferencia con centro en el origen. Antes de empezar, es importante entender algunos conceptos básicos de geometría y álgebra.

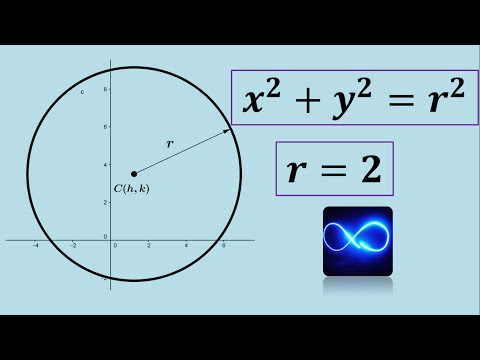
Una circunferencia con centro en el origen se caracteriza por tener todos sus puntos equidistantes al origen (0,0). La ecuación general de una circunferencia con centro en el origen es:

x^2 + y^2 = r^2

Donde (x, y) son las coordenadas de un punto en la circunferencia y r es el radio de la misma.

Para calcular la ecuación de una circunferencia con centro en el origen, necesitamos conocer el radio. Si se nos proporciona el radio, podemos sustituir el valor de r en la ecuación general y obtener la ecuación específica.

Por ejemplo, si el radio de la circunferencia es 5 unidades, la ecuación de la circunferencia sería:

x^2 + y^2 = 5^2
x^2 + y^2 = 25

Es importante tener en cuenta que la ecuación de una circunferencia con centro en el origen siempre tendrá el término constante igual a cero.

Si se nos proporcionan las coordenadas de un punto en la circunferencia, podemos encontrar el radio utilizando la fórmula de la distancia entre dos puntos. Esta fórmula es:

d = sqrt((x2 – x1)^2 + (y2 – y1)^2)

Donde (x1, y1) y (x2, y2) son las coordenadas de dos puntos en la circunferencia y d es la distancia entre ellos. Como el centro de la circunferencia es el origen, podemos tomar uno de los puntos como (0, 0), y la fórmula se simplifica a:

d = sqrt(x^2 + y^2)

Si conocemos la distancia entre el origen y un punto en la circunferencia, podemos utilizar esta fórmula para encontrar el radio.

Una vez que tenemos el radio, podemos sustituir su valor en la ecuación general de la circunferencia y obtener la ecuación específica.

Cómo encontrar la ecuación general de la circunferencia

Cómo calcular la ecuación de una circunferencia con centro en el origen

En el campo de la geometría, las circunferencias son una figura muy común y se utilizan en una amplia variedad de aplicaciones. Calcular la ecuación de una circunferencia con centro en el origen es un proceso relativamente sencillo pero que requiere de algunos conceptos básicos de álgebra y geometría.

La ecuación general de una circunferencia se define como (x – h)^2 + (y – k)^2 = r^2, donde (h, k) son las coordenadas del centro de la circunferencia y r es el radio. En el caso de una circunferencia con centro en el origen, las coordenadas del centro son (0, 0) y la ecuación se simplifica a x^2 + y^2 = r^2.

Para calcular el radio de la circunferencia, se necesita conocer algún punto sobre la misma. Supongamos que tenemos un punto (x, y) sobre la circunferencia. Sustituimos estas coordenadas en la ecuación de la circunferencia y resolvemos para r.

Tomando el punto (x, y), la ecuación se convierte en x^2 + y^2 = r^2. Sustituyendo las coordenadas del punto, la ecuación se convierte en x^2 + y^2 = x^2 + y^2. Como puedes observar, las x^2 y las y^2 se cancelan y nos queda 0 = 0. Esto significa que el radio r puede tener cualquier valor real.

Cuál es la ecuación de la circunferencia que tiene centro en el origen y radio igual a 4

Cómo calcular la ecuación de una circunferencia con centro en el origen

En este artículo, vamos a explicar cómo calcular la ecuación de una circunferencia que tiene su centro en el origen y un radio dado. Este tipo de circunferencia se caracteriza por tener todos sus puntos equidistantes del origen, con una distancia igual al radio.

La ecuación general de una circunferencia en un sistema de coordenadas cartesianas es (x – h)^2 + (y – k)^2 = r^2, donde (h, k) representa las coordenadas del centro de la circunferencia y r es el radio.

En el caso de una circunferencia con centro en el origen, las coordenadas del centro son (0, 0), por lo que la ecuación se simplifica a x^2 + y^2 = r^2.

Si el radio de la circunferencia es igual a 4, la ecuación sería x^2 + y^2 = 4^2.

Para calcular los puntos de la circunferencia, podemos hacer una tabla con valores de x y y que satisfagan la ecuación. Tomando valores para x desde -4 hasta 4, podemos calcular los valores correspondientes de y utilizando la ecuación.

Tabla de valores:

• x = -4, y = √(4^2 – (-4)^2) = √(16 + 16) = √32
• x = -3, y = √(4^2 – (-3)^2) = √(16 + 9) = √25 = 5
• x = -2, y = √(4^2 – (-2)^2) = √(16 + 4) = √20 ≈ 4.47
• x = -1, y = √(4^2 – (-1)^2) = √(16 + 1) = √17 ≈ 4.12
• x = 0, y = √(4^2 – 0^2) = √16 = 4
• x = 1, y = √(4^2 – 1^2) = √(16 + 1) = √17 ≈ 4.12
• x = 2, y = √(4^2 – 2^2) = √(16 + 4) = √20 ≈ 4.47
• x = 3, y = √(4^2 – 3^2) = √(16

  ¡Así que ahí lo tienes! Calcular la ecuación de una circunferencia con centro en el origen no es tan difícil como parece. Solo tienes que seguir estos pasos y estarás dibujando circunferencias como un verdadero matemático. ¡Que viva la geometría y que las ecuaciones circulares te acompañen siempre! ¡Hasta la próxima, calculadoras de circunferencias!