Cómo encontrar el punto inicial de un vector: guía paso a paso

¿Alguna vez te has preguntado cómo encontrar el punto inicial de un vector? Si eres nuevo en el mundo de la física, las matemáticas o la programación, puede parecer un desafío. Pero no te preocupes, en este artículo te daremos una guía paso a paso para que puedas encontrar fácilmente el punto inicial de cualquier vector. Desde conceptos básicos hasta ejemplos prácticos, te guiaremos a través de este proceso de manera clara y concisa. Así que prepárate para adentrarte en el fascinante mundo de los vectores y descubrir cómo localizar su punto inicial. ¡Comencemos!

Cuál es el punto inicial de un vector

Cómo encontrar el punto inicial de un vector: guía paso a paso

En el ámbito de la física y las matemáticas, los vectores son una herramienta fundamental para representar magnitudes con dirección y magnitud. Los vectores se componen de dos elementos importantes: el punto inicial y el punto final. En este artículo, te explicaremos cómo encontrar el punto inicial de un vector de manera sencilla y paso a paso.

¿Qué es el punto inicial de un vector?

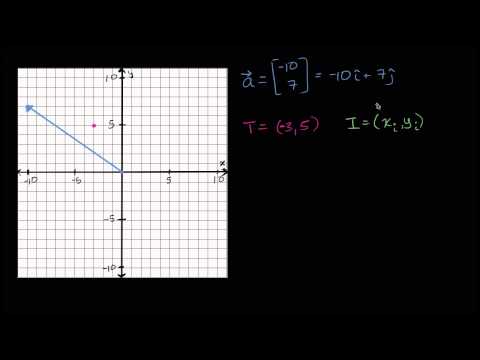
El punto inicial de un vector es el punto de partida desde el cual se inicia la dirección y magnitud del vector. Es esencial para comprender y representar correctamente el vector en un sistema de coordenadas. En un plano bidimensional, se puede representar como un par ordenado (x, y) donde x y y son las coordenadas del punto inicial.

Pasos para encontrar el punto inicial de un vector

A continuación, te presentamos una guía paso a paso para encontrar el punto inicial de un vector:

1. Identifica el vector: Antes de encontrar el punto inicial, debes identificar el vector en cuestión. El vector se representa con una flecha que indica su dirección y magnitud.
2. Obtén las coordenadas del punto final: El punto final del vector es el punto donde la flecha termina. Debes conocer las coordenadas (x, y) del punto final para poder encontrar el punto inicial.
3. Utiliza la regla del paralelogramo: La regla del paralelogramo establece que si tienes dos vectores iguales, pero con puntos finales diferentes, puedes encontrar el punto inicial trazando un paralelogramo con los dos vectores. El punto donde se encuentran las diagonales del paralelogramo es el punto inicial.
4. Aplica la fórmula de traslación: Si el vector no tiene un punto final específico, puedes utilizar la fórmula de traslación para encontrar el punto inicial. Esta fórmula te permite desplazar el vector a un nuevo origen, lo que te permitirá identificar el punto inicial.

Ejemplo práctico

Para ilustrar mejor el proceso, veamos un ejemplo práctico:

Supongamos que tenemos un vector V con un punto final en las coordenadas (3, 4). Para encontrar el punto inicial, podemos seguir los siguientes pasos:

1. Ident
   

   Cómo mover un vector al origen

   Cómo encontrar el punto inicial de un vector: guía paso a paso

   En el mundo de la física y la geometría, los vectores son una herramienta fundamental para describir magnitudes con dirección y sentido. Un vector se representa mediante una flecha que indica su dirección y su magnitud. Sin embargo, en algunas ocasiones puede resultar útil mover un vector al origen para facilitar su análisis y cálculo. En este artículo, te enseñaremos cómo encontrar el punto inicial de un vector paso a paso.

   Antes de comenzar, es importante recordar que un vector se compone de dos componentes principales: la magnitud y la dirección. La magnitud representa la longitud del vector, mientras que la dirección indica hacia dónde apunta. En este caso, nos centraremos en encontrar el punto inicial del vector, es decir, el punto desde el cual se origina.

   El primer paso para encontrar el punto inicial de un vector es identificar sus componentes. Para ello, necesitamos conocer la magnitud del vector y su dirección. La magnitud se expresa mediante un número positivo, mientras que la dirección se indica mediante un ángulo en relación con algún punto de referencia, como el eje x.

   Una vez que tenemos identificadas las componentes del vector, podemos utilizar trigonometría para descomponer el vector en sus componentes rectangulares. Esto nos permitirá determinar las coordenadas del punto inicial del vector. Para ello, utilizaremos las siguientes fórmulas:

   x = magnitud * cos(angulo)
   y = magnitud * sin(angulo)

   Donde «x» y «y» representan las coordenadas del punto inicial del vector, «magnitud» es la magnitud del vector y «angulo» es el ángulo de dirección del vector.

   Una vez que hemos calculado las coordenadas del punto inicial del vector, podemos representarlo gráficamente en un plano cartesiano. Esto nos permitirá visualizar de manera más clara la posición del punto inicial en relación con otros elementos del sistema.

   Cómo se representa un punto en el espacio R3

   Cómo se representa un punto en el espacio R3

   En el espacio tridimensional R3, un punto se representa mediante un conjunto ordenado de tres coordenadas, también conocidas como coordenadas cartesianas. Estas coordenadas corresponden a las posiciones del punto a lo largo de los ejes x, y, y z.

   Para representar un punto en R3, se utiliza una notación específica. Por ejemplo, si queremos representar el punto P con coordenadas (x, y, z), podemos escribirlo como P(x, y, z).

   El eje x se extiende horizontalmente hacia la derecha, el eje y se extiende verticalmente hacia arriba y el eje z se extiende hacia afuera del plano, formando una línea perpendicular al plano x-y.

   Para encontrar el punto inicial de un vector en R3, es necesario tomar en cuenta las coordenadas del vector. Un vector se representa mediante una dirección y una magnitud. La dirección del vector se puede expresar utilizando ángulos o mediante las componentes del vector en las direcciones x, y, y z.

   Si tenemos un vector v con componentes (a, b, c), su punto inicial se encuentra en el origen del sistema de coordenadas (0, 0, 0). Esto se debe a que el punto inicial de un vector siempre coincide con el origen del sistema de coordenadas.

   Por lo tanto, para encontrar el punto inicial de un vector v, simplemente debemos considerar que sus componentes son las coordenadas del punto inicial. Es decir, el punto inicial del vector v será P(a, b, c).

   ¡Así que ahí lo tienes, mi amigo! Ahora ya sabes cómo encontrar el punto inicial de un vector como un verdadero experto. No más perdidas en el espacio vectorial, ¡estás listo para trazar tu camino hacia el origen con confianza! Recuerda, en el mundo de los vectores, siempre es importante saber de dónde vienes para llegar a dónde quieres ir. ¡Buena suerte en tus próximas aventuras matemáticas!