El teorema de los ejes paralelos: concepto y aplicaciones

El teorema de los ejes paralelos es una herramienta fundamental en el campo de la electrónica y la ingeniería en general. Permite comprender y analizar el comportamiento de los circuitos eléctricos con mayor precisión y eficiencia. En este artículo, exploraremos en detalle el concepto de este teorema, así como sus diversas aplicaciones prácticas. Descubriremos cómo este principio puede simplificar el diseño y la resolución de problemas en sistemas eléctricos complejos. ¡Prepárate para sumergirte en el fascinante mundo de los ejes paralelos y su relevancia en la electrónica moderna!

Qué establece el teorema de los ejes paralelos

El teorema de los ejes paralelos es un principio fundamental en la física y la ingeniería que establece una relación entre el momento de inercia de un objeto y el momento de inercia de un conjunto de objetos que giran alrededor de un eje paralelo. Este teorema, también conocido como el teorema de Steiner, es de gran importancia en el diseño de estructuras y maquinaria, así como en la comprensión del movimiento de objetos en rotación.

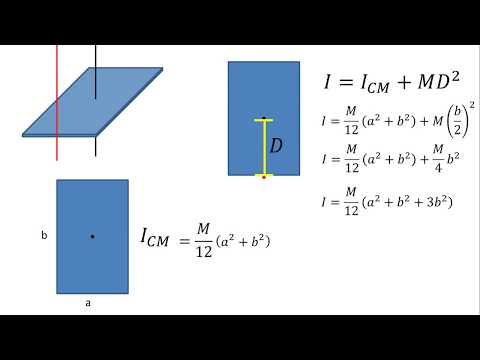
El concepto básico del teorema de los ejes paralelos es que el momento de inercia de un objeto en relación a un eje que pasa por su centro de masa es igual a la suma del momento de inercia de ese objeto en relación a un eje paralelo más el producto de su masa por la distancia al cuadrado entre los dos ejes. Matemáticamente, esto se expresa como:

I_cm = I_paralelo + md²

Donde I_cm es el momento de inercia del objeto con respecto al eje que pasa por su centro de masa, I_paralelo es el momento de inercia del objeto con respecto al eje paralelo y m es la masa del objeto. La distancia d representa la distancia entre los dos ejes paralelos.

Este teorema tiene muchas aplicaciones prácticas en diversos campos de la ingeniería y la física. En el diseño de estructuras, por ejemplo, el teorema de los ejes paralelos permite calcular de manera eficiente el momento de inercia de un conjunto de elementos que forman una estructura compleja. Esto es especialmente útil en el análisis de la resistencia y la estabilidad de las estructuras.

En la ingeniería mecánica, el teorema de los ejes paralelos es esencial para comprender el movimiento de objetos en rotación. Al conocer el momento de inercia de un objeto en relación a su centro de masa y aplicar el teorema de los ejes paralelos, es posible calcular el momento de inercia del objeto en relación a cualquier otro eje paralelo. Esta información es fundamental para el diseño y la optimización de máquinas y dispositivos que involucran movimiento rotatorio.

Dónde se aplica el teorema de ejes paralelos

El teorema de los ejes paralelos: concepto y aplicaciones

El teorema de los ejes paralelos es un principio fundamental en el campo de la física y la ingeniería, que se aplica en diversos ámbitos relacionados con la mecánica, la electricidad y la electrónica. Este teorema establece una relación importante entre los momentos de inercia de un objeto en diferentes ejes de rotación paralelos.

Concepto básico

El teorema de los ejes paralelos, también conocido como el teorema de Steiner, establece que el momento de inercia de un objeto con respecto a un eje paralelo a otro eje de rotación puede calcularse sumando el momento de inercia del objeto con respecto a su centro de masa y el producto de su masa por la distancia al cuadrado entre los dos ejes paralelos.

Matemáticamente, podemos expresar el teorema de los ejes paralelos de la siguiente manera:

I_paralelo = I_cm + md²

Donde:

• I_paralelo es el momento de inercia del objeto con respecto al eje paralelo.
• I_cm es el momento de inercia del objeto con respecto a su centro de masa.
• m es la masa del objeto.
• d es la distancia entre los dos ejes paralelos.

Aplicaciones prácticas

El teorema de los ejes paralelos tiene diversas aplicaciones en diferentes disciplinas de la ingeniería y la física. Algunas de las aplicaciones más comunes son:

• Rotación de cuerpos rígidos: El teorema de los ejes paralelos se utiliza para calcular el momento de inercia de objetos en rotación alrededor de ejes paralelos. Esto es especialmente útil en el diseño de máquinas y estructuras que requieren un análisis detallado de su comportamiento dinámico.
• Estabilidad de sistemas mecánicos: El teorema de los ejes paralelos también se aplica en el estudio de la estabilidad de sistemas mecánicos, como por ejemplo
  

  Cuándo se aplica el teorema de Steiner

  El teorema de los ejes paralelos: concepto y aplicaciones

  El teorema de los ejes paralelos, también conocido como el teorema de Steiner, es una herramienta fundamental en el campo de la mecánica y la ingeniería. Este teorema establece que el momento de inercia de un cuerpo alrededor de un eje paralelo a su eje de simetría se puede calcular sumando el momento de inercia del cuerpo alrededor de su eje de simetría más el producto de su masa por la distancia al cuadrado entre los dos ejes.

  En otras palabras, el teorema de Steiner nos permite calcular el momento de inercia de un cuerpo alrededor de un eje paralelo a su eje de simetría, sin necesidad de realizar complicados cálculos geométricos. Este teorema es especialmente útil cuando se trabaja con cuerpos de formas irregulares o complicadas.

  El teorema de los ejes paralelos tiene diversas aplicaciones en la práctica. Una de las aplicaciones más comunes es en el diseño y análisis de sistemas mecánicos, como por ejemplo en el cálculo de momentos de inercia de ejes de rotación en maquinaria industrial.

  Además, el teorema de Steiner también se utiliza en el campo de la física, especialmente en mecánica clásica. Por ejemplo, en el estudio del movimiento de un cuerpo rígido alrededor de un eje paralelo a su eje de simetría, el teorema de los ejes paralelos nos permite calcular el momento de inercia total del cuerpo y así determinar su comportamiento dinámico.

  Otro campo en el que el teorema de Steiner es ampliamente utilizado es la ingeniería estructural. En el diseño de estructuras como puentes o edificios, es necesario tener en cuenta el momento de inercia de los elementos estructurales para garantizar su estabilidad y resistencia ante las cargas aplicadas. El teorema de los ejes paralelos facilita el cálculo de estos momentos de inercia, lo que permite optimizar el diseño de las estructuras.

  ¡Así que ahí lo tienes! El teorema de los ejes paralelos es como el mejor amigo del mundo de la electrónica. Nos ayuda a mantener todo en orden y evitar que nuestros circuitos se vuelvan locos. Ya sea que estemos hablando de motores, resistencias o incluso robots, este teorema siempre está ahí para asegurarse de que todo esté en su lugar. Así que la próxima vez que te encuentres lidiando con un montón de cables enredados, recuerda al teorema de los ejes paralelos y verás cómo todo se vuelve mucho más sencillo. ¡Feliz electrónica!